Công thức tính diện tích hình vuông rất đơn giản, nhưng nếu đã lâu không sử dụng, nhiều người có thể quên cách tính. Nếu bạn đang tìm kiếm công thức và cách tính diện tích hình vuông, mời bạn theo dõi cách tính và ví dụ minh họa sau đây.
Dưới đây là khái niệm, tính chất và cách tính diện tích hình vuông cùng ví dụ minh họa. Mời bạn theo dõi.
Khái niệm hình vuông
Trong hình học Euclid, hình vuông được định nghĩa là một hình tứ giác đều, có thể coi là một hình chữ nhật có các cạnh bằng nhau, hoặc là một hình thoi có hai đường chéo bằng nhau.
Tính chất của hình vuông
- Hai đường chéo bằng nhau, vuông góc và gặp nhau tại trung điểm của mỗi đường.
- Điểm giao của các đường phân giác, trung tuyến, trung trực đều trùng nhau tại một điểm.
- Một đường chéo chia hình vuông thành hai phần có diện tích bằng nhau.
- Hình vuông có một đường tròn nội tiếp và một đường tròn ngoại tiếp. Tâm của cả hai đường tròn này đều trùng nhau và là điểm giao của hai đường chéo của hình vuông.
- Hình vuông cũng có tất cả các tính chất của hình chữ nhật, hình bình hành và hình thoi.
Dấu hiệu nhận biết
- Hình chữ nhật có hai cạnh liền kề bằng nhau.
- Hình thoi có một góc vuông.
- Hình thoi có hai đường chéo bằng nhau.
- Hình chữ nhật có hai đường chéo vuông góc.
- Hình chữ nhật có một đường chéo là phân giác của một góc.
Công thức tính diện tích hình vuông
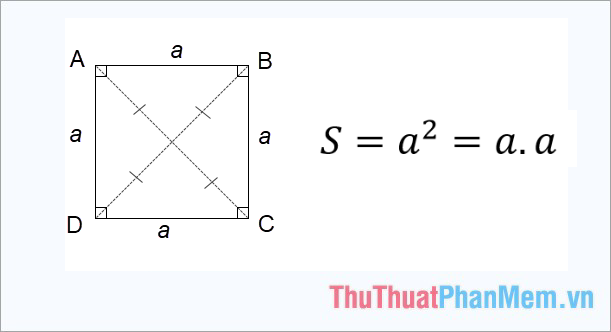
Diện tích của hình vuông bằng bình phương của độ dài cạnh: \(S = {a^2} = a.a\)
Trong công thức trên: S là diện tích của hình vuông, a đại diện cho độ dài cạnh của hình vuông.
Phương pháp tính diện tích hình vuông
- Để tính diện tích hình vuông, trước tiên bạn cần biết độ dài cạnh của nó, đại diện là a. Nếu đề bài cung cấp độ dài cạnh, bạn không cần phải thực hiện bước này.
- Sau khi có độ dài cạnh a, bạn sử dụng công thức diện tích hình vuông là \(S = {a^2}\) để tính toán.
Ví dụ minh họa
Ví dụ 1: Cho hình vuông ABCD có độ dài cạnh là 6 cm, hãy tính diện tích của hình vuông ABCD.
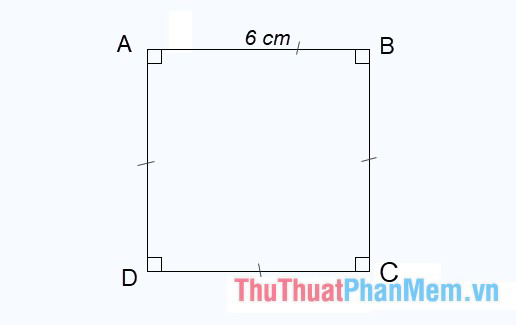
Theo yêu cầu của đề bài, ta có giá trị a = 6.
Áp dụng công thức tính diện tích hình vuông \(S = {a^2} = {6^2} = 36c{m^2}\).
Ví dụ 2: Cho hình vuông ABCD với đường chéo độ dài là \(5\sqrt 2 \) cm, hãy tính diện tích hình vuông ABCD.
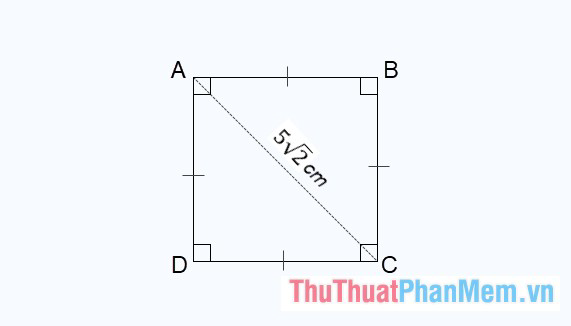
Theo yêu cầu của đề bài, chúng ta có AC = \(5\sqrt 2 \)
Áp dụng định lý Pythagoras \(A{C^2} = A{B^2} + B{C^2}\)
Vì AB = BC => \(A{C^2} = A{B^2} + A{B^2} = 2A{B^2}\)
\( \Rightarrow AB = \sqrt {\frac{{A{C^2}}}{2}} = \frac{{AC}}{{\sqrt 2 }} = \frac{{5\sqrt 2 }}{{\sqrt 2 }} = 5cm\)
Vậy độ dài cạnh của hình vuông là a = 5,
Sử dụng công thức tính diện tích hình vuông: \(S = {a^2} = {5^2} = 25c{m^2}\)
Trên đây là bài viết chia sẻ về khái niệm hình vuông, tính chất, dấu hiệu nhận biết, công thức và cách tính diện tích hình vuông cùng ví dụ minh họa. Hy vọng bạn sẽ ghi nhớ và áp dụng khi cần thiết. Chúc bạn thành công!