Bạn chưa hiểu rõ về độ dốc của đường thẳng và đang cần tính? Hãy tham khảo ngay bài viết này để hiểu rõ hơn về độ dốc và cách tính nó.

Dưới đây là bài viết chia sẻ về độ dốc và cách tính độ dốc của đường thẳng, mời bạn cùng theo dõi.
Độ dốc của đường thẳng
Trong mặt phẳng tọa độ Oxy, độ dốc của đường thẳng (d) là tan α, trong đó α là góc tạo bởi đường thẳng (d) và trục Ox.
• Nếu \(\alpha \ne {90^o}\) thì k = tan α chính là độ dốc của đường thẳng (d).
- Nếu k > 0 thì 0 < α < 90°
- Nếu k < 0 thì 90° < α < 180°
• Nếu \(\alpha = {90^o}\) \(\left( {d \bot Ox} \right)\) thì đường thẳng (d) không có độ dốc vì tan 90° không xác định.
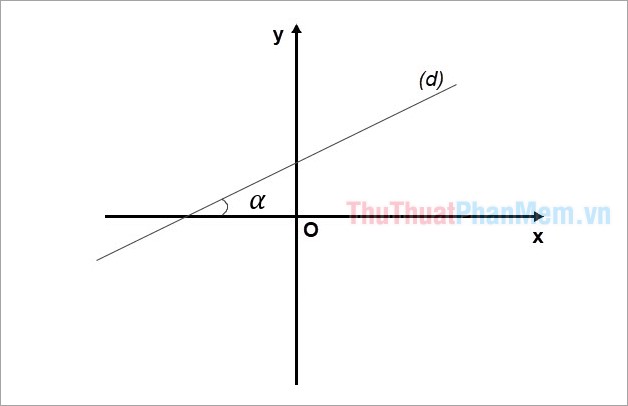
Phát biểu 1: Đường thẳng (d) có độ dốc là k có dạng y = kx + b
Phát biểu 2: Đường thẳng (d) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và có độ dốc là k có phương trình là \(y = k\left( {x - {x_0}} \right) + {y_0}\)
Hai đường thẳng song song hoặc trùng nhau sẽ có cùng độ dốc.
Cách tính độ dốc của đường thẳng
Như vậy, đường thẳng (d) có dạng chung là (d): Ax + By + C = 0
Nếu \(B \ne 0\), ta đổi đường thẳng (d) thành dạng: y = kx + b
\( \Leftrightarrow \frac{A}{B}x + y + \frac{C}{B} = 0\)
\( \Rightarrow y = - \frac{A}{B}x - \frac{C}{B}\)
Khi đó độ dốc của đường thẳng (d) là \(k = - \frac{A}{B}\)
Cách tính góc a tạo bởi đường thẳng (d) và trục Ox
Để tính góc α, ta cần biết độ dốc k của đường thẳng, sử dụng cách tính độ dốc đã nêu. Sau khi có độ dốc k, ta có: tan α = k => α
Ví dụ thực hành
Ví dụ 1: Cho đường thẳng (d): 2y - x + 1 = 0, hãy xác định độ dốc của đường thẳng (d) và tính góc giữa đường thẳng d và trục Ox.
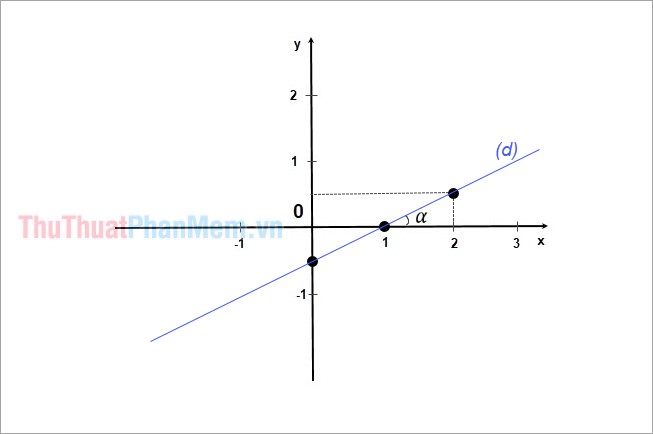
Giải
Ta có: 2y - x + 1 = 0
\( \Leftrightarrow 2y = x - 1\)
\( \Leftrightarrow y = \frac{1}{2}x - \frac{1}{2}\)
=> Độ dốc của đường thẳng (d) là \(k = \frac{1}{2}\)
Và vì tan \(\alpha = k = \frac{1}{2}\)
\( \Rightarrow \alpha = \arctan \frac{1}{2}\)
Do đó góc giữa đường thẳng d và trục Ox là \(\arctan \frac{1}{2}\)
Ví dụ 2: Cho hàm số y = -x + 2
a) Vẽ đồ thị của hàm số.
b) Tính góc tạo bởi đường thẳng y = -x + 2 và trục Ox (làm tròn đến phút).
Giải
Đồ thị của hàm số:
x = 0 => y = 2 , điểm A(0; 2)
y = 0 => x = 2 , điểm B(2; 0)
Đường thẳng y = - x + 2 là đồ thị của hàm số đi qua hai điểm A(0; 2) và B(2; 0).
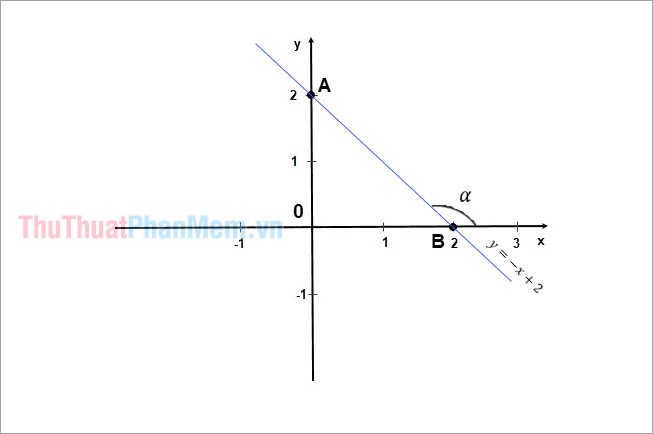
Góc tạo bởi đường thẳng y = - x + 2 và trục Ox là α
\( \Rightarrow \alpha = \widehat {ABx}\)
\(\vartriangle OAB\) là tam giác vuông cân vì OA=OB
\( \Rightarrow \widehat {OBA} = \widehat {OAB} = {45^o}\)
Do đó \(\alpha = {180^o} - \widehat {OBA} = {180^o} - {45^o} = {135^o}\)
=> Góc tạo bởi đường thẳng y = - x + 2 và trục Ox là 135°
Ví dụ 3: Cho hàm số y = -2x + 3
Tính góc giữa đường thẳng y và trục Ox (làm tròn đến phút).
Giải
Đồ thị của hàm số y = -2x + 3
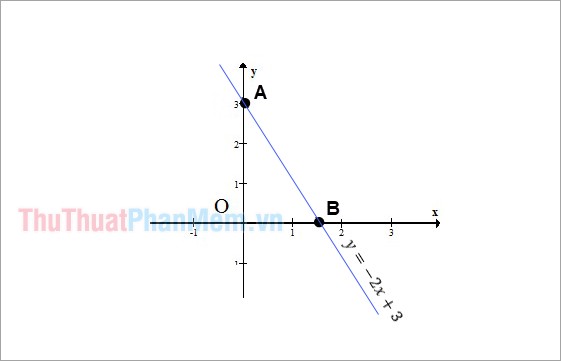
Gọi α là góc tạo bởi đường thẳng y = -2x + 3 và trục Ox.
\( \Rightarrow \alpha = \widehat {ABx}\)
Cho tam giác vuông OAB, ta có: \(\tan \widehat {OBA} = \frac{{OA}}{{OB}} = 2\)
\( \Rightarrow \widehat {OBA} = {63^o}26'\)
\( \Rightarrow \alpha = {180^o} - \widehat {OBA} = {180^o} - \,{63^o}26' = {116^o}34'\)
Góc tạo bởi đường thẳng y = -2x + 3 và trục Ox là \({116^o}34'\)
Ở đây Minprice đã chia sẻ về hệ số góc của đường thẳng và cách tính hệ số góc của đường thẳng kèm ví dụ cụ thể. Hy vọng sau bài viết này các bạn sẽ hiểu rõ hơn về hệ số góc và cách tính hệ số góc của đường thẳng. Chúc các bạn thành công!