
Dễ hiểu rằng: Bạn không nên cố gắng chiếm đóng thế giới. Tuy nhiên, nếu bạn vẫn quyết làm điều đó, cuốn sách mới của Ryan North có một số ý tưởng thú vị về cách có được sức mạnh siêu ác nhân. Nếu bạn chọn con đường làm ác nhân, chắc chắn bạn sẽ cần có căn cứ của riêng mình. Trong khi cuốn sách chứa nhiều ý tưởng, tôi thích nhất là khả năng của một quả cầu kim loại lớn nổi lên.
Bạn có thể đã nhận ra rằng kim loại không nổi lên trong không khí, ít nhất là không bình thường. Nhưng nếu bạn xây dựng một cái gì đó giống như một quả bóng bay với vỏ kim loại thay vì làm từ cao su, liệu điều đó có thể hoạt động không? Có. Đúng vậy.
Làm thế nào để Vật Thể Nổi Lên?
Bắt đầu với điều gì đó đơn giản: một quả bóng tiệc được bơm đầy helium. Hãy tưởng tượng dây bóng cân bằng với một số trọng lượng để nó nổi hoàn hảo. Nó không nâng lên và không rơi xuống—nó chỉ đứng đó đợi khách mời ngắm nghía. Nhưng điều gì khiến nó ở đó? Câu trả lời là sự kết hợp giữa lực hấp dẫn và không khí xung quanh.
Hãy tưởng tượng bạn có thể nhìn vào không khí rất kỹ và thấy nó như nó thực sự là—một đám phân tử, chủ yếu là nitrogen và một số oxy. Những phân tử này giống như những quả bóng di chuyển xung quanh theo mọi hướng. Khi có điều gì đó đứng trước đường chúng, như một bức tường hoặc cao su của quả bóng, chúng va chạm vào nó và nảy lại. Vì phân tử thay đổi chuyển động trong suốt quá trình này, phải có một lực từ bức tường đẩy lên phân tử. (Lực luôn là tương tác giữa hai đối tượng, trong trường hợp này là phân tử và bức tường.) Vì bức tường đẩy lên phân tử, phải có một lực ngược lại từ phân tử đẩy lên bức tường.
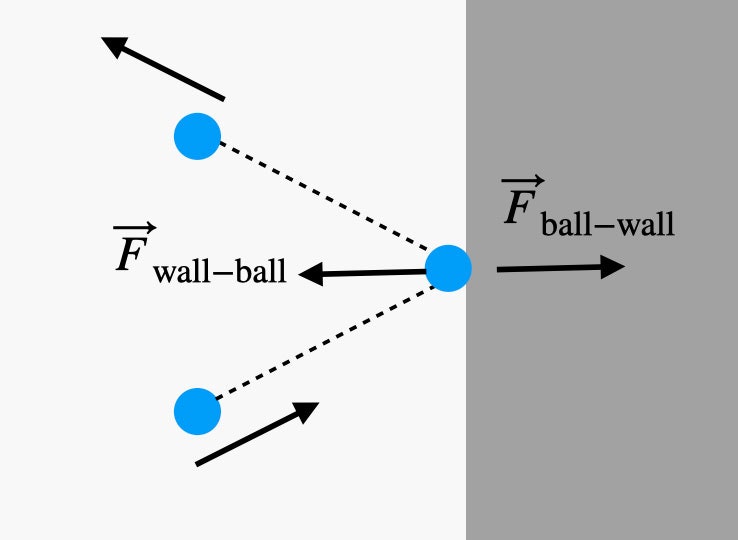
Tất nhiên, đó chỉ là một cuộc va chạm. Thực tế sẽ có nhiều cuộc va chạm với bức tường (vì có nhiều phân tử không khí). Tổng lực tác động lên bức tường từ không khí phụ thuộc vào số cuộc va chạm—và số cuộc va chạm phụ thuộc vào kích thước của bức tường. Một bức tường lớn rõ ràng sẽ có nhiều cuộc va chạm.
Vì vậy, thay vì nói về tổng lực tác động lên bức tường, việc nhìn vào lực (F) trên mỗi đơn vị diện tích (A) sẽ dễ hơn một chút. Chúng ta gọi đây là áp suất (P). Trong trường hợp này, đó sẽ là áp suất của không khí.
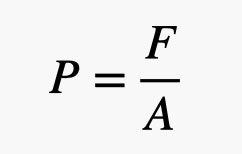
Nhưng chờ đã! Áp suất cũng phụ thuộc vào khối lượng của phân tử, tốc độ của chúng và số lượng phân tử trong khí (đó là mật độ). Chúng ta thực sự không cần phải quá lo lắng về khối lượng của phân tử không khí trừ khi chúng ta thay đổi khí. (Nếu kế hoạch của bạn để chiếm lấy thế giới bao gồm việc thay đổi khí quyển từ nitrogen-oxy sang cái gì đó khác, đó có lẽ không phải là một kế hoạch siêu tuyệt vời.) Và tốc độ của chúng liên quan trực tiếp đến nhiệt độ không khí, vì vậy bạn có thể tăng tốc chúng bằng cách làm nóng không khí.
Mật độ không khí là yếu tố quan trọng nhất. Giả sử quả bóng của bạn có đường kính 10 centimet, đó là một kích thước tiệc vui thú vị. Mật độ không khí ở phía trên quả bóng thấp hơn mật độ ở phía dưới, tạo ra sự chênh lệch áp suất. Gần mức biển, áp suất không khí là khoảng 105 N/m2 (14.7 psi). Vì vậy, chuyển từ phía dưới quả bóng lên trên sẽ tạo ra một thay đổi áp suất là 1.176 N/m2.
Hãy sử dụng sự thay đổi này trong áp suất để tính toán một số lực. Tôi sẽ làm một điều hơi kỳ lạ—tôi sẽ sử dụng một quả bóng hình hộp. (Nếu điều đó làm bạn hoảng sợ, tôi hiểu.) Tuy nhiên, điều này sẽ là một phép tính đơn giản hơn nhiều, và điều tương tự cũng áp dụng với một quả bóng hình cầu có kích thước L x L x L.
Dưới đây là quả bóng:
quả bóng vuông
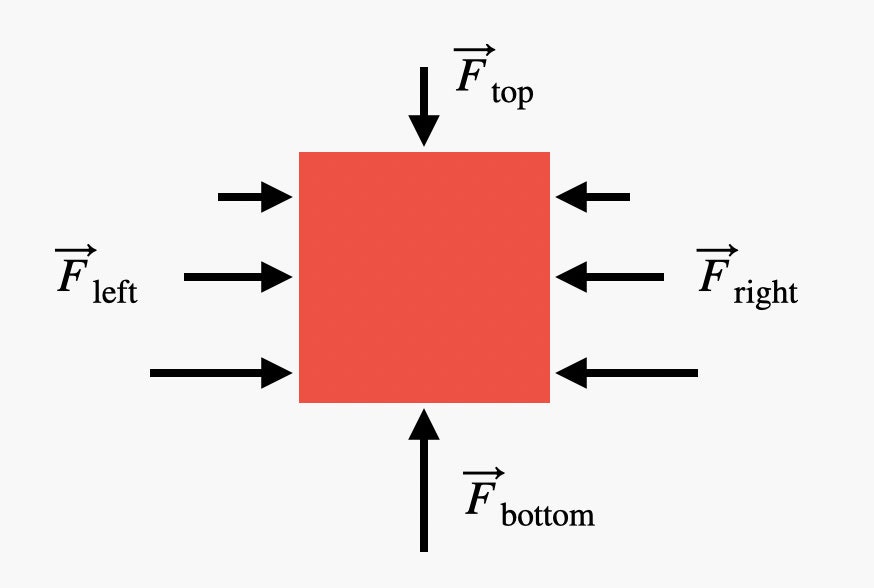
(Tôi chỉ hiển thị các lực do áp suất từ không khí.)
Hãy bắt đầu với bốn bề mặt dọc của quả bóng hình hộp. Vì chúng là dọc, áp suất ở phía dưới khác áp suất ở phía trên. Việc tính toán lực tổng trên những bề mặt này là có thể, nhưng không phải là dễ dàng. Nhìn vào lực trên bên trái của quả bóng, chúng ta có thể thấy rằng chúng hoàn toàn trái ngược với lực trên bên phải của quả bóng. Khi cộng dồn những lực trái-phải này lại, chúng hủy bỏ nhau. Điều tương tự sẽ xảy ra với hai bề mặt dọc còn lại của hình hộp (phía trước và phía sau). Vì vậy, chúng ta không cần phải lo lắng về chúng.
Còn phần dưới của quả bóng? Bề mặt này ở một độ cao không đổi (vì nó là một bề mặt nằm ngang), nên việc tính toán lực do áp suất không khí là dễ dàng. Chúng ta chỉ cần diện tích của A, tức là L2. Điều này tạo ra một lực đẩy lên là:

Tôi có thể làm chính xác điều đó cho phần trên của quả bóng—nhưng lực này đang đẩy xuống và áp suất ở phía trên ít hơn một chút. Điều này tạo ra lực ròng theo hướng dọc như sau:
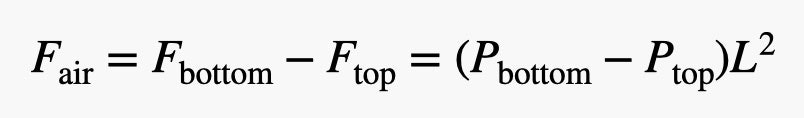
Hãy nhớ rằng sự thay đổi áp suất phụ thuộc vào sự chênh lệch độ cao. Chúng ta có thể viết sự thay đổi áp suất này như sau:
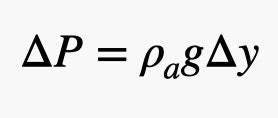
Trong biểu thức này, ρa là khối lượng riêng của không khí ở phía dưới của quả bóng (khoảng 1.2 kilogram mỗi mét3), và g là trường trọng lực (9.8 newton mỗi kilogram). Đối với quả bóng hình hộp, sự thay đổi chiều cao (Δy) bằng L.
Ghép tất cả lại, chúng ta có được:
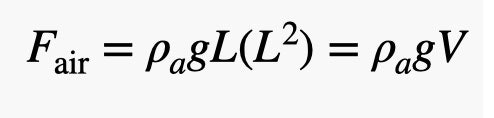
Có, tôi đã thay thế L3 bằng V—thể tích của hình hộp. Chúng ta có một lực đẩy lên trên chiếc hình hộp này do sự thay đổi áp suất của không khí. Vì điều này sử dụng mật độ của không khí và thể tích không khí bị tr displaced, chúng ta có thể nói rằng lực đẩy lên tương đương với trọng lượng không khí bị tr displaced. Thường chúng ta gọi điều này là lực nổi. (Nhưng, hãy nhớ rằng đó là do không khí—đó là lý do tôi thích Fair.)
Điều này hoạt động cho bất kỳ đối tượng có hình dạng nào nơi V là thể tích. Lưu ý rằng tổng lực này từ không khí chỉ phụ thuộc vào các va chạm giữa các phân tử không khí và bề mặt. Không quan trọng vật liệu của quả bóng là gì hoặc nó được điền vào cái gì. Chỉ có thể tích là quan trọng.
Vậy tại sao một quả bóng đám cưới nổi lên nhưng một quả bóng rổ cùng kích thước lại rơi xuống? Điều này liên quan đến việc lực đẩy nổi đi lên có đủ để vượt qua lực hấp dẫn đang kéo đối tượng xuống.
Hãy thêm vào một số con số. Hãy giả sử cả một quả bóng rổ và một quả bóng cưới có đường kính là 20 cm. Tính thể tích và đưa vào công thức Fair, tôi có một lực đẩy lên có giá trị là 0.049 newtons. Đó là rất nhỏ.
Nhưng vỏ cao su của một chiếc bóng bay mỏng, vì vậy lực hấp dẫn không lớn. Và nếu bạn bơm nó bằng helium, một loại khí có mật độ thấp hơn không khí, bạn có thể đền bù cho khối lượng của bề mặt mỏng của bóng và đạt được sự cân bằng. Nếu bạn có thể làm cho khối lượng của cao su cộng với khí helium bằng với lực đẩy nổi đẩy lên, thì bóng sẽ nổi lên.
Không quan trọng bạn đặt gì vào quả bóng rổ; nó vẫn sẽ rơi. Vỏ cao su của quả bóng rổ dày và nặng hơn nhiều so với bề mặt của quả bóng bay. Lực đẩy nổi nhỏ gần như không đáng kể so với lực hấp dẫn đối với một đối tượng có khối lượng này và nó không thể vượt qua. Vì vậy, quả bóng rơi xuống.
Xây Dựng Nơi Ẩn Nấp Nổi
Bây giờ, hãy làm việc trên nơi ẩn nấp siêu ác của bạn. Ryan North khẳng định rằng nếu bạn tạo một quả cầu kim loại rỗng đủ lớn, bạn có thể biến nó thành một căn cứ nổi bí mật để sử dụng trong khi bạn cố gắng chiếm đóng thế giới. Hoặc có lẽ bạn chỉ muốn ngồi đó, tôi không biết.
Có thực sự khả thi không?
Hãy tạo một vật hình cầu và xem nó có nổi không. Hãy nhớ rằng để vật nổi, trọng lượng của nó phải bằng với trọng lượng của không khí được đẩy lùi. Đối với vật này, nó sẽ có hai phần - vỏ ngoại và khí bên trong. Khí bên trong sẽ có bán kính là R và mật độ ρ~1~. Vỏ có độ dày t với mật độ là ρ2.
Việc đầu tiên (và đơn giản) để tính là lực đẩy nổi. Điều này chỉ phụ thuộc vào thể tích của cả quả cầu, có bán kính là R + t. Nhưng nếu chúng ta sẽ có được căn cứ siêu ác này, nó sẽ chỉ hoạt động với một lớp vỏ mỏng. Điều đó có nghĩa là chúng ta chỉ cần nói rằng bán kính của cả thứ là giống như bán kính bên trong (R).
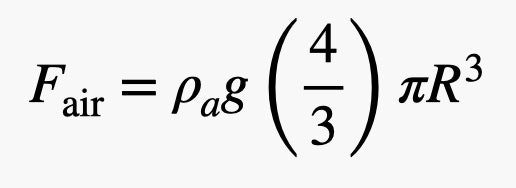
Ở đây, tôi đang sử dụng phương trình cho thể tích của một quả cầu, đó là nơi mà 4/3 đến từ. Đừng lo lắng, sau này chúng ta có thể đặt một số con số vào.
Bây giờ là trọng lượng của quả cầu này. Điều này sẽ phụ thuộc vào thể tích của khí, mật độ của khí cũng như thể tích và mật độ của vật liệu vỏ.
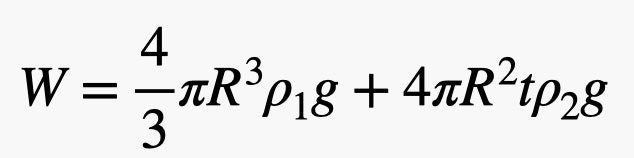
Tôi đã sử dụng một thủ thuật nhỏ ở đây. Đối với thể tích của lớp vỏ, tôi giả định rằng nó mỏng. Điều này có nghĩa là thể tích có thể được ước lượng như là diện tích bề mặt của bóng bay nhân với độ dày. (Có một công thức tốt hơn cho thể tích của lớp vỏ, nhưng nó trở nên hơi lộn xộn.)
Nếu tôi làm cho trọng lượng của cả quả cầu bằng với lực đẩy nổi từ không khí, chúng ta có được một căn cứ nổi, nhưng chú ý rằng tôi không chỉ định giá trị của R. Chúng ta có thể biến đổi bán kính tổng, loại khí bên trong, độ dày của lớp vỏ và mật độ của lớp vỏ.
Giả sử tôi muốn xây dựng một quả cầu nổi bằng nhôm có độ dày 5 cm (với mật độ là 2.7 gram mỗi centimet^3) và điền nó bằng một loại khí ít dày hơn không khí một chút - như 1.0 thay vì 1.2 kg/m3.
(Bạn cũng có thể thực hiện điều này với chính không khí, chỉ cần giảm lượng không khí trong quả cầu. Bạn vẫn có thể thở bên trong nó, nhưng sẽ khó khăn hơn, như khi bạn đứng ở độ cao cao trên đỉnh núi.)
Để xác định kích thước cần phải làm cho nó nổi, tôi đã tạo một chương trình Python ngắn.
Nó ra kích thước với đường kính hơn 4 km, hoặc 2.5 dặm. Đó là một căn cứ thực sự lớn. Sẽ rất khó để giữ cho điều gì đó như vậy là một bí mật, nhưng nó thật sự sẽ tuyệt vời.
Bạn có thể cố gắng làm cho nó nhỏ hơn với một số thay đổi. Đầu tiên, hãy giảm mật độ của khí bên trong xuống còn 0.8 kg/m^3 và sử dụng một lớp vỏ dày chỉ 3 cm. Trong trường hợp đó, bạn có được một quả cầu với đường kính là 1.2 km (0.75 dặm). Đó là tốt hơn một chút.
Các tính toán này giả định rằng mật độ không khí giảm theo độ cao một cách tuyến tính. Nhưng khi bạn lên rất cao, không khí trở nên siêu mỏng - mật độ của nó gần như bằng không khi bạn đạt tới không gian bên ngoài.
Vậy liệu việc xây lair ngay tại ranh giới của tầng khí quyển Trái Đất có thể cho phép bạn tạo ra một quả cầu nổi với kích thước dễ quản lý hơn không? Tôi e rằng không. Vì không khí ở phía trên của quả cầu đẩy xuống và không khí ở phía dưới đẩy lên, nên lực nổi thực sự phụ thuộc vào cách mật độ thay đổi chứ không phải giá trị thực tế của mật độ. Ở độ cao siêu cao, mật độ không thể xuống dưới 0, vì vậy sự thay đổi mật độ không thể lớn. Điều này có nghĩa là bạn không thể tạo ra căn cứ siêu ác nhân của mình ở mép không gian. Bạn cần phải là một siêu ác nhân ở độ cao thấp hơn.
Nhưng hoàn toàn có thể đưa căn cứ của bạn nổi lên gần mức độ của đám mây, chúng giữ cho mình nổi lên mặc dù được tạo ra từ nước. Đám mây sẽ làm cho trụ sở của bạn khó nhận diện hơn, đặc biệt nếu bạn làm cho căn cứ của mình giống như một trong số chúng.
Vậy, cuối cùng, căn cứ nổi này có thể khả thi, nhưng có lẽ không rất thực tế. Điều đó cũng ổn. Hy vọng rằng việc chiếm lấy thế giới sẽ luôn khó khăn.
Các Bài Viết Tuyệt Vời Khác Từ MINPRICE
- 📩 Tin tức mới nhất về công nghệ, khoa học và nhiều hơn nữa: Nhận bản tin của chúng tôi!
- Sức ảnh hưởng vô tận của người đại diện của Facebook tại Washington
- Tất nhiên, chúng ta đang sống trong một mô phỏng
- Một cược lớn để chấm dứt mật khẩu mãi mãi
- Cách chặn cuộc gọi và tin nhắn rác
- Sự kết thúc của việc lưu trữ dữ liệu vô tận có thể giúp bạn tự do
- 👁️ Khám phá trí tuệ nhân tạo như chưa bao giờ có với cơ sở dữ liệu mới của chúng tôi
- ✨ Tối ưu hóa cuộc sống gia đình của bạn với những lựa chọn tốt nhất từ đội ngũ Gear của chúng tôi, từ robot hút bụi đến nệm giá rẻ đến loa thông minh