Cách tính bán kính của đường tròn và ví dụ minh họa

Đường tròn thường xuất hiện trong toán học và không nắm vững kiến thức về nó có thể gây khó khăn khi giải bài tập. Hãy cùng tìm hiểu cách tính bán kính của đường tròn và ví dụ minh họa dưới đây để cải thiện kiến thức của bạn.

I. Định nghĩa về đường tròn

Đường tròn là tập hợp các điểm trên mặt phẳng, cách một điểm cho trước với một khoảng cách nhất định. Điểm này gọi là tâm và khoảng cách gọi là bán kính.

Để định nghĩa một đường tròn, chúng ta cần biết tâm và bán kính của nó hoặc một đoạn thẳng là đường kính. Khi biết 3 điểm không thẳng hàng, ta có thể vẽ được một và chỉ một đường tròn.

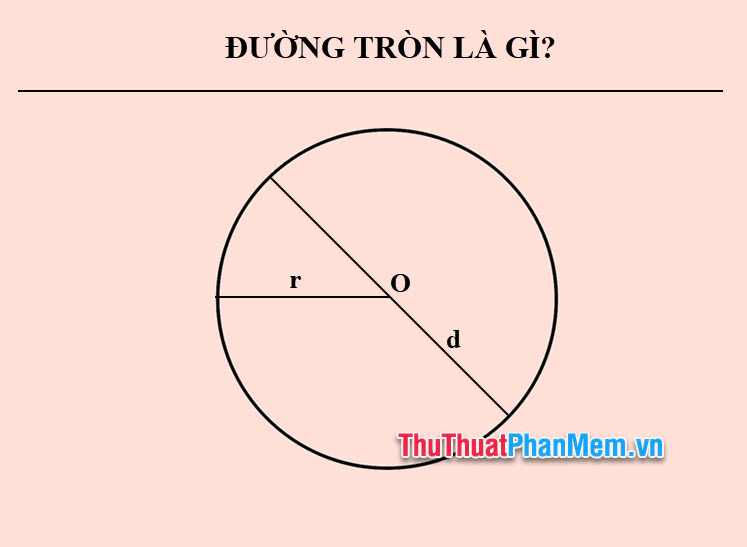
Khác biệt giữa đường tròn và hình tròn là rất rõ ràng. Hình tròn bao gồm tất cả các điểm nằm trong và trên đường tròn hoặc các điểm cách tâm không quá bán kính. Đường tròn không có diện tích như hình tròn.

Bán kính của đường tròn là đoạn thẳng nối từ tâm đến một điểm bất kì trên đường tròn và bằng một nửa đường kính.

Đường kính của đường tròn là đoạn thẳng có hai đầu mút nằm trên đường tròn và là dây cung đi qua tâm hoặc là khoảng cách lớn nhất giữa hai điểm trên đường tròn. Đường kính bằng hai lần bán kính.

Đường tròn ngoại tiếp đa giác là đường tròn đi qua tất cả các đỉnh của đa giác. Khi vẽ một đường tròn đi qua các đỉnh của đa giác, ta có đường tròn ngoại tiếp đa giác.

Đường tròn nội tiếp đa giác là đường tròn tiếp xúc với tất cả các cạnh của đa giác. Đường tròn này được vẽ bên trong đa giác sao cho các cạnh của đa giác là tiếp tuyến của đường tròn.

II. Công thức tính bán kính đường tròn ngoại tiếp tam giác

1. Định nghĩa về đường tròn ngoại tiếp tam giác

Đường tròn ngoại tiếp tam giác là đường tròn tiếp xúc với bên ngoài của tam giác hoặc đi qua ba đỉnh của tam giác. Tâm của đường tròn ngoại tiếp là giao điểm của ba đường trung trực của tam giác. Nó cũng có thể được gọi là tam giác nội tiếp đường tròn.

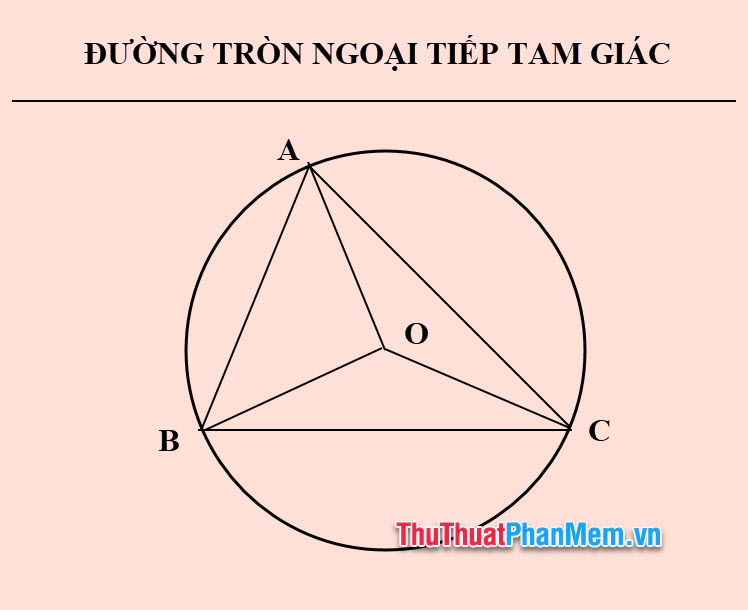
Tính chất của đường tròn ngoại tiếp tam giác

• Mỗi tam giác chỉ có một và chỉ một đường tròn ngoại tiếp
• Giao điểm của ba đường trung trực trong tam giác chính là tâm của đường tròn ngoại tiếp
• Trong tam giác vuông, tâm của đường tròn ngoại tiếp là trung điểm của cạnh huyền
• Trong tam giác đều, tâm đường tròn ngoại tiếp và nội tiếp của tam giác là cùng một điểm

2. Công thức tính bán kính đường tròn ngoại tiếp tam giác

Bán kính của đường tròn ngoại tiếp tam giác là khoảng cách từ tâm của đường tròn đến một trong ba đỉnh của tam giác. Khi nối tâm O của đường tròn với ba đỉnh của tam giác ABC, ta thu được ba đoạn thẳng: OA = OB = OC, chính là bán kính của đường tròn ngoại tiếp tam giác ABC.

Có 4 phương pháp tính bán kính đường tròn ngoại tiếp tam giác tùy thuộc vào dữ liệu của đề bài. Cho tam giác ABC với S là diện tích, R là bán kính đường tròn ngoại tiếp, a, b, c là độ dài các cạnh, O là tâm của đường tròn ngoại tiếp tam giác ABC, ta có:

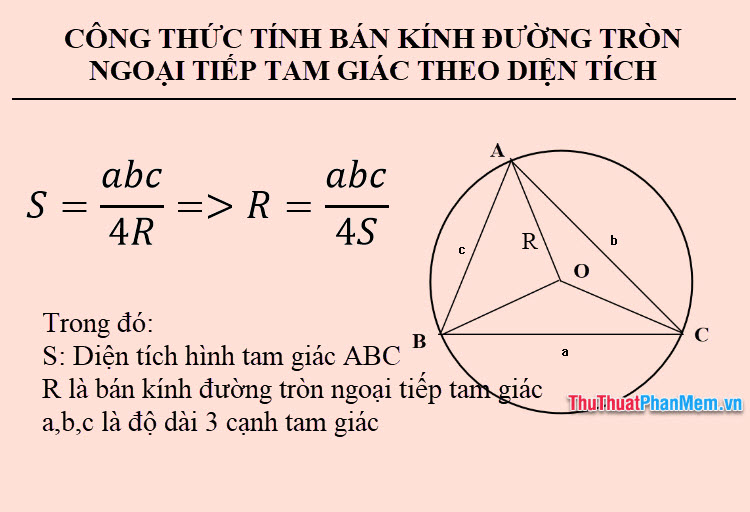
Công thức tính bán kính đường tròn ngoại tiếp tam giác theo diện tích

Trong tam giác ABC, bán kính R của đường tròn ngoại tiếp tam giác ABC được tính dựa trên độ dài các cạnh của tam giác với công thức: R = √(abc/4S)

Cách tính bán kính đường tròn ngoại tiếp tam giác bằng phương pháp hệ tọa độ

Bước 1: Xác định tọa độ của tâm O của đường tròn ngoại tiếp tam giác ABC

Bước 2: Tìm tọa độ của một trong ba đỉnh A, B, C (nếu chưa biết)

Bước 3: Tính khoảng cách từ tâm O đến một trong ba đỉnh A, B, C, kết quả chính là bán kính cần tìm: R = OA = OB = OC.

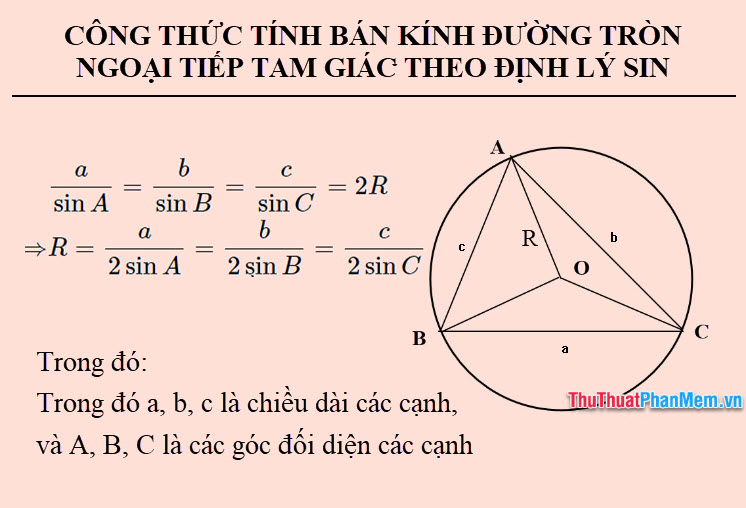
Công thức tính bán kính đường tròn ngoại tiếp tam giác dựa trên định lý sin

Áp dụng định lý sin trong tam giác, ta có:

asinA=bsinB=csinC=2R⇒R=a2sinA=b2sinB=c2sinC

Trong đó a, b, c là độ dài các cạnh, và A, B, C là các góc đối diện với các cạnh.

Cách tính bán kính đường tròn ngoại tiếp tam giác vuông

Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền, do đó bán kính của đường tròn ngoại tiếp tam giác vuông chính bằng một nửa độ dài của cạnh huyền.

3. Ví dụ minh họa

Ví dụ: Trong tam giác ABC, góc A là 45° và BC = 4 cm. Hãy tính bán kính của đường tròn ngoại tiếp tam giác ABC.

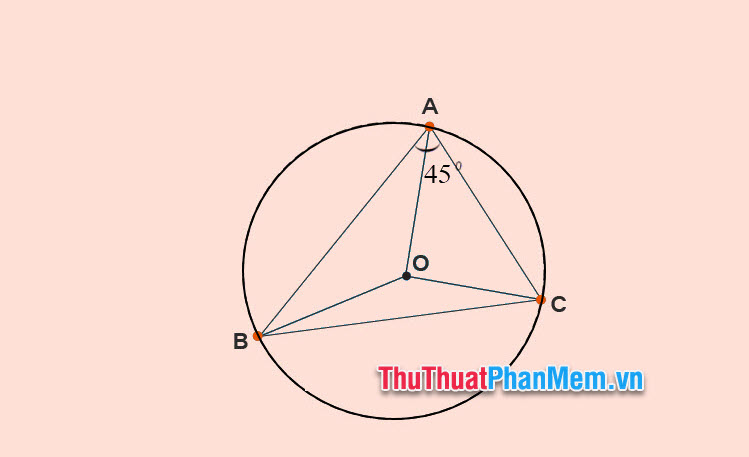
Giải

Đặt R là bán kính của đường tròn ngoại tiếp tam giác ABC.

Cho a = BC = 4

Áp dụng định lý sin trong tam giác ABC, ta có: asina=2R

=>R=a2sina=42sin45∘=42sina=4√2=2√2

Bán kính của đường tròn ngoại tiếp tam giác ABC là 2√2 cm.

Ví dụ 2: Trong tam giác ABC, AB = 6, BC = 8 và CA = 10. Hãy tính bán kính của đường tròn ngoại tiếp tam giác ABC.

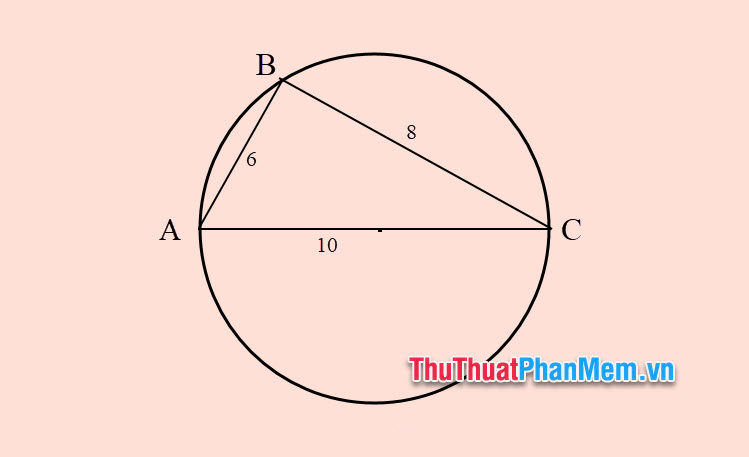
Giải

Có AB2=62=36;BC2=82=64;AC2=102=100

Vì 36 + 64 = 100

Nên AB2+BC2=AC2, theo định lý Pytago thì tam giác ABC vuông tại B.

Bán kính của đường tròn ngoại tiếp tam giác ABC là:

R=12AC=12×10=5 cm

III. Công thức tính bán kính đường tròn nội tiếp tam giác

1. Định nghĩa

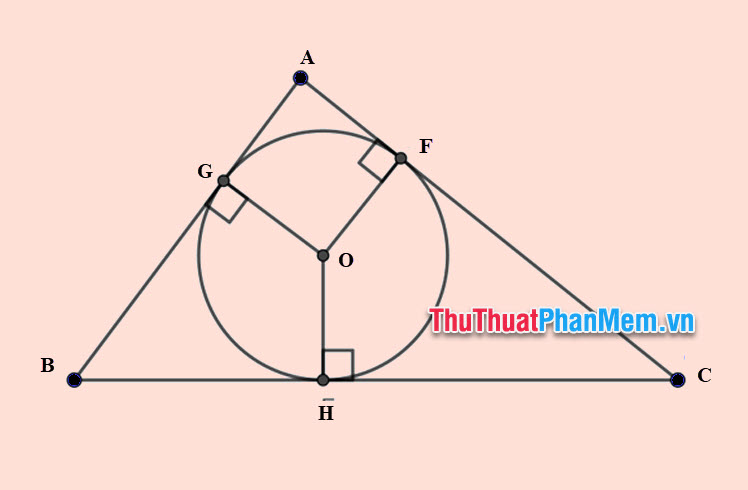
Tính chất của đường tròn nội tiếp tam giác

• Mỗi tam giác chỉ có một đường tròn nội tiếp
• Đối với tam giác đều, đường tròn ngoại tiếp và nội tiếp có cùng tâm
• Tâm của đường tròn nội tiếp là giao điểm của 3 đường phân giác

2. Công thức tính bán kính đường tròn nội tiếp tam giác

Công thức tính bán kính đường tròn nội tiếp theo diện tích và chu vi tam giác: r=Sp=2Sa+b+c

Trong đó:

• a, b, c là độ dài ba cạnh tương ứng với BC, AC, AB
• p là nửa chu vi: p=a+b+c2
• S là diện tích của tam giác
• r là bán kính đường tròn nội tiếp tam giác

3. Ví dụ minh họa

Ví dụ 3: Cho tam giác ABC có AB = 7, AC = 8 và BC = 13. Tính bán kính đường tròn nội tiếp tam giác ABC.

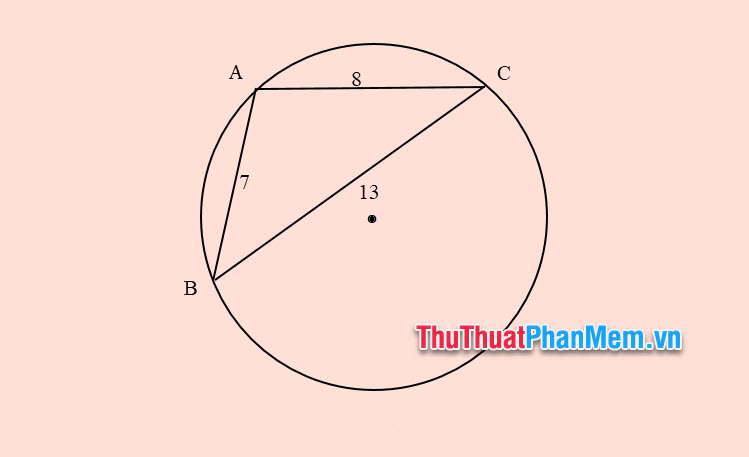
Bài giải

Ta tính nửa chu vi tam giác ABC:

p=AB+AC+BC2=7+8+132 = 14

Theo công thức Heron, diện tích tam giác ABC là:

S=√p(p−AB)(p−AC)(p−BC)=√14⋅(14−7)(14−8)(14−13)=√14⋅(14.7.6.1)=√588=24√1214

Áp dụng công thức tính bán kính đường tròn nội tiếp tam giác, ta có:

r=Sp=24√1214=12√127

Ví dụ 4: Cho tam giác ABC có ˆE=60∘ và AB = 6, BC = 12.

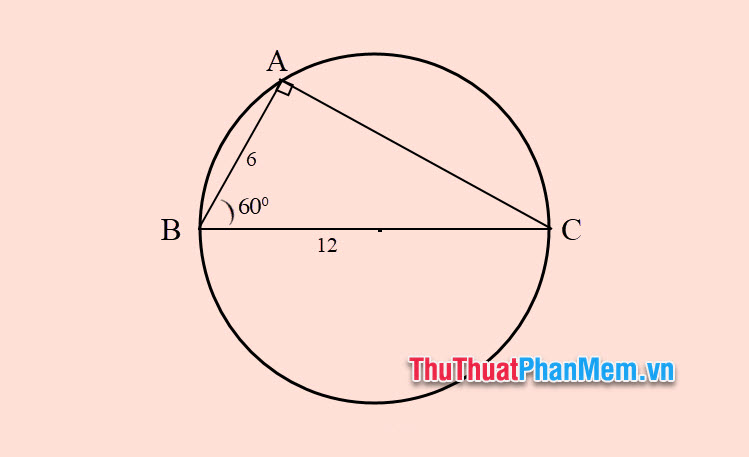
a. Tìm độ dài cạnh AC.

b. Tìm diện tích tam giác ABC.

c. Tính bán kính đường tròn nội tiếp tam giác ABC.

Bài giải

a. Sử dụng định lý Cosin cho tam giác ABC ta có:

AC² = AB²+BC² - 2*AB*BC*cos(E)

AC² = 6²+12² - 2*6*12*cos(60⁰)

AC² = 36 + 144 -72 = 108

=>AC=√108=6√3

b. Ta có: AB2=62=36;AC2=108;BC2=122=144

Ta thấy 36 + 108 = 144. Do đó AB2+AC2=BC2

Kết luận tam giác ABC vuông tại A.

Diện tích tam giác ABC là: S=12AB⋅AC=6⋅6√3=18√3

c. Nửa chu vi tam giác ABC là: p=AB+AC+BC2=6+6√3+122=9+3√3

Áp dụng công thức tính bán kính đường tròn nội tiếp tam giác ABC là:

r=Sp=18√39+3√3=3√3−3

Vậy bán kính đường tròn nội tiếp tam giác ABC là: 3√3−3

Bài viết đã cung cấp công thức tính bán kính đường tròn ngoại và nội tiếp tam giác, cùng với ví dụ minh họa. Hy vọng bạn đã nắm vững kiến thức và có thể áp dụng vào giải các bài tập thực tế. Cảm ơn bạn đã theo dõi.